Zad. 1. Woda, zamieniając się w lód, zwiększa objętość o 1/11. O ile zmniejszy się objętość lodu, który zamienia się w wodę?
Zad. 2. Państwo Kowalscy odnawiają mieszkanie. Mąż na pomalowanie ścian potrzebuje 14 dni, a wspólnie z żoną pomalowaliby je w ciągu 10 dni. Ile dni na pomalowanie ścian potrzebowałaby sama żona?
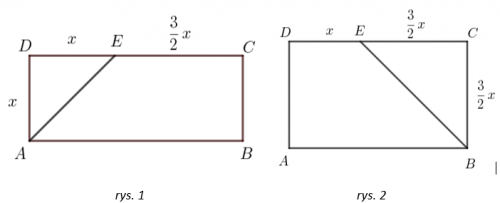
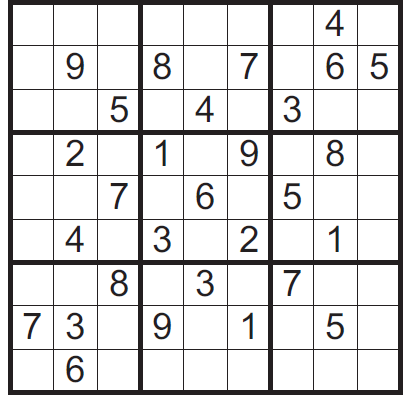
Zad. 3. Prostokąt ma obwód 112 cm. Dwusieczna jednego z jego kątów wewnętrznych dzieli dłuższy bok w stosunku 2:3. Oblicz długości boków tego prostokąta.
W czerwcu punkty zdobyli:
- 3 – Darya Karnitskaya SP 107 Wrocław;
- 2,5 – Adam Kosarzycki SP 16 Wrocław, Yaraslau Sialiuk SP 82 Wrocław, Wiktor Szwarczyński SP Szkoła w Chmurze Poznań;
- 2 – Adam Gajdzis SP 107 Wrocław, Anita Głowacz SP Popielów, Paweł Jarzyński SP 13 Zielona Góra, Alicja Picińska SP 64 Wrocław, Kacper Ziółek SP 2 Szczytno;
- 1,5 – Ignacy Włodarski SP 36 Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Z jednej części wody otrzymujemy 12/11 części lodu, a z jednej części lodu otrzymujemy 1:12/11=11/12 części wody. Część lodu, który zamienia się w wodę zmniejsza swą objętość o 1/12 tej części.
Zad. 2. Mąż maluje codziennie 1/14 część wszystkich ścian, zaś 1/10 gdy maluje razem z żoną. Żona, więc maluje samodzielnie 1/10-1/14=1/35 część wszystkich ścian. Sama zatem na pomalowanie ścian potrzebuje 35 dni.
Zad. 3. Dwusieczna AE odcina od prostokąta równoramienny trójkąt prostokątny AED. Z warunków zadania wynika, że |DE|:|EC|=2:3. Przyjmijmy, że |AD|=x, wówczas |DE|=x oraz |EC|=3/2x. Wiedząc, że obwód prostokąta równy jest 112 otrzymujemy, ze x=16=|AD| oraz |DC|=x+3/2x=40. Boki prostokąta mają długości 16 i 40 cm. Natomiast, jeśli BE jest dwusieczną kąta (rys. 2) wówczas x=14 i boki prostokąta wynoszą 21 i 35 cm.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
