Zad. 1. Wykaż, że dla każdej liczby naturalnej większej od 1 zachodzi nierówność
Zad. 2. Funkcja f o dziedzinie rzeczywistej spełnia dla wszystkich a, b nierówność
|f(a)−f(b)|≤|a−b|. Wykaż, że jeśli f(f(f(0)))=0, to f(0)=0.
Zad. 3. Wykaż, że dla każdej liczby naturalnej n istnieje taka liczba naturalna k, że suma liczb od n do n+k (włącznie) jest kwadratem.
W tym miesiącu 11 pkt. zdobył Szymon Michalik, SP 3 Przymierza Rodzin Warszawa.
Zad. 1. Skorzystamy z nierówności między średnimi geometryczną i arytmetyczną wielu liczb. Mamy
|b|=|b−0|=|f(a)−f(b)|≤|a−b|=|f(0)−f(a)|≤|0−a|=|a|
W obu przypadkach otrzymujemy a=0, co stanowi tezę zadania.
Zad. 3. Pokażemy, że taką liczbą jest 2n−2. Skorzystamy z faktu, że 1+2+...+a = a(a+1)/2.


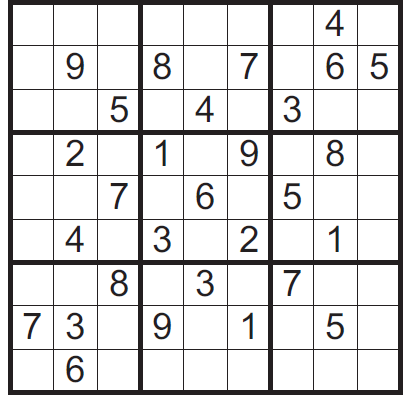
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


